Year 6 Poster Competition
Target Audience: All year 6 students from Cornwall, Devon, Dorset and Somerset.
Format: Students create an A3 poster on a theme selected by us. The posters are judged by EMS students and winners announced at the end of the summer term.
Aim: To get creative with maths.
How to get involved: Information is sent to all primary schools in our catchment area, timed perfectly to use post-SATS. Teachers can request to be added to our mailing list by emailing events@exeterms.ac.uk
Capacity: No limit at the moment!
The Year 6 Poster Competition makes a welcome return this year with the theme of Ancient Egyptian Fractions.
Schools can send as many entries as they like, with students entered as individuals or in teams of up to 4.
Full details of the competition are linked below, including helpful starting points. Participants are encouraged to explore the suggested avenues and whatever other avenues take their interest.
The deadline for entries is Monday 26th June.
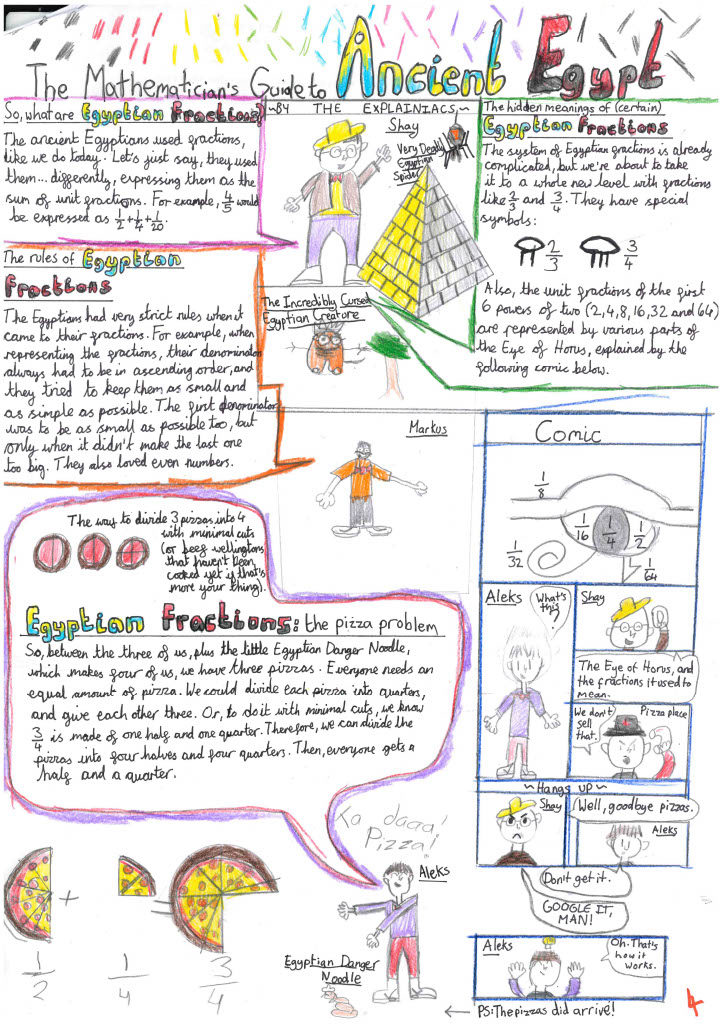
Ancient Egyptian Fractions was the theme for this year’s poster competition, leading to some eye-catching designs from our primary school competitors. We were as delighted as ever by the quality of design, research and mathematics on display; well done to everyone that took part.
Marks were awarded for mathematical content, creativity and overall presentation. After much wrangling and careful analysis by our year 12 students, the following posters emerged triumphant:
First Place: 4 – Eastover Primary School
Judges’ comments – The winning poster impressed with it’s creativity and was particularly praised for its comic book illustrations, which was interesting, intuitive and unique.
Second Place: 65 – Pilgrim Primary Academy
Judges’ comments – The second place poster scored highly for it’s beautiful art and presentation, with lots of good maths and workings.

Third Place: 124 – Blackbrook Primary
Judges’ comments – The judges loved the colourful entry for third place and noted that it was one of the few entries to really delve into the rich history of Egyptian Fractions.

Special Mention also goes to 66 – Blackbrook Primary and 87 – Bishop Cornish CoE VA Primary School who narrowly missed out on a place in the top three. The judges appreciated the level of information shared, along with their striking designs.
66 – Blackbrook Primary

87 – Bishop Cornish CoE VA Primary School








